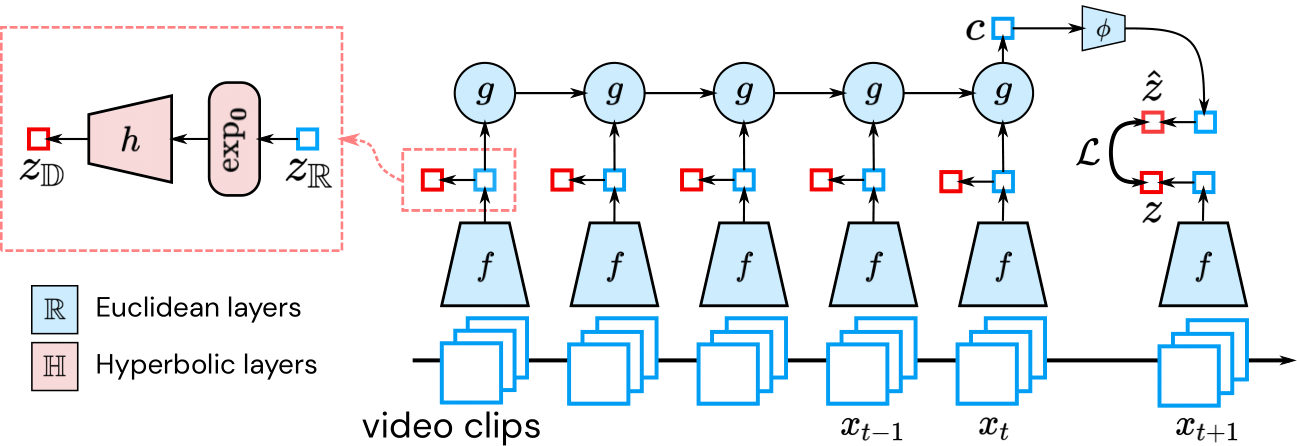
Learning the Predictability of the Future
Columbia University
CVPR 2021
We introduce a framework for learning from unlabeled video what is predictable in the future. Instead of committing up front to features to predict, our approach learns from data which features are predictable.
Based on the observation that hyperbolic geometry naturally and compactly encodes hierarchical structure, we propose a predictive model in hyperbolic space. When the model is most confident, it will predict at a concrete level of the hierarchy, but when the model is not confident, it learns to automatically select a higher level of abstraction. Experiments on two established datasets show the key role of hierarchical representations for action prediction. Although our representation is trained with unlabeled video, visualizations show that action hierarchies emerge in the representation.
Paper

@InProceedings{suris2021hyperfuture,
title={Learning the Predictability of the Future},
author={Sur\'is, D\'idac and Liu, Ruoshi and Vondrick, Carl},
journal={Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
year={2021}
}
Predictability as a Hierarchy
The key contribution of this paper is to predict a hierarchical representation of the future. When the future is certain, our model should predict the future z as specifically as possible. However, when the future is uncertain, our model should “hedge the bet” and forecast a hierarchical parent of z. Informally, hyperbolic space can be viewed as the continuous analog of a tree. Since this space is naturally suited for hierarchies, hyperbolic predictive models are able to smoothly interpolate between forecasting abstract representations (in the case of low predictability) to concrete representations (in the case of high predictability).
The future is non-deterministic. Given a specific past (first three frames in the figure), different representations (represented by squares in the Poincaré ball) can encode different futures, all of them possible. In case the model is uncertain, it will predict an abstraction of all these possible futures, represented by ẑ (red square). The more confident it is, the more specific the prediction can get. Assuming the actual future is represented by z (blue square), the gray arrows represent the trajectory the prediction will follow as more information is available. The pink circle exemplifies the increase in generality when computing the mean of two specific representations (pink squares).

Results
Play on full screen for a better visualization.
Analysis
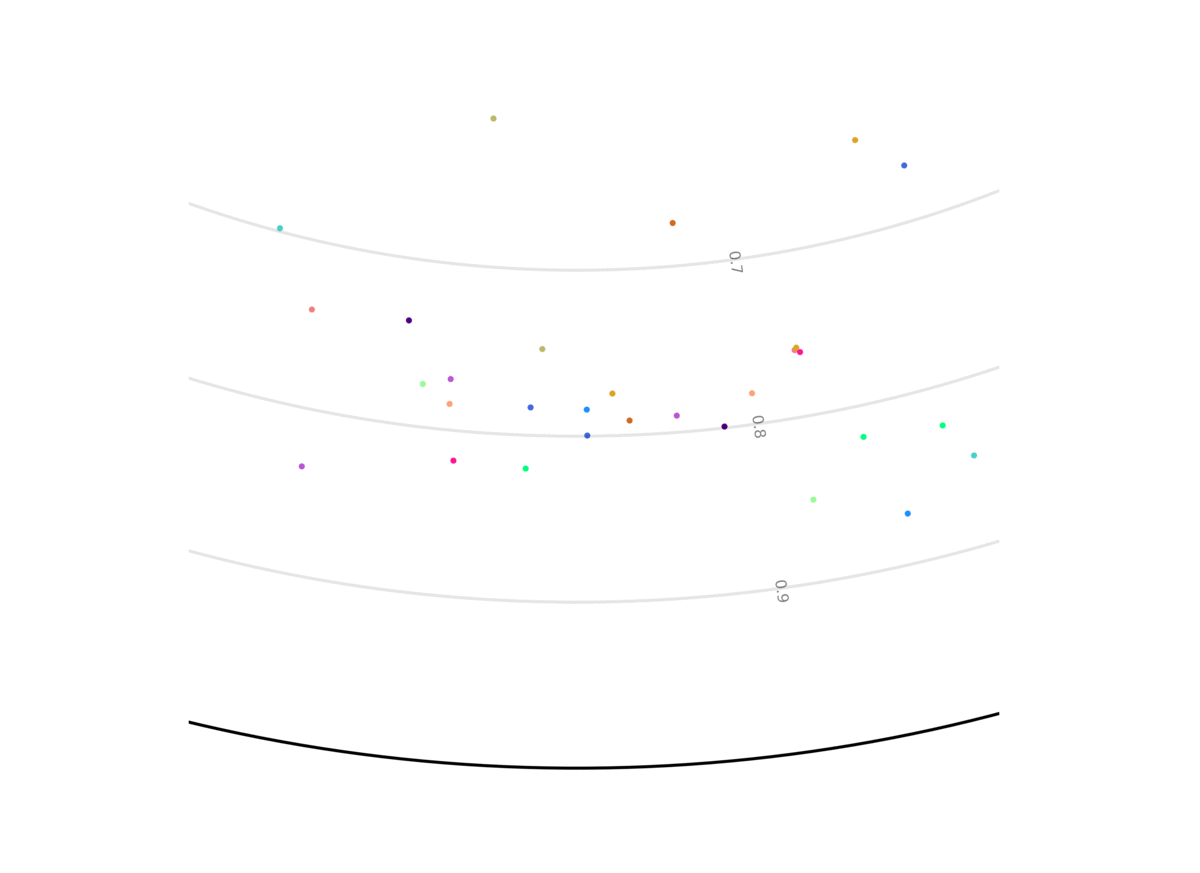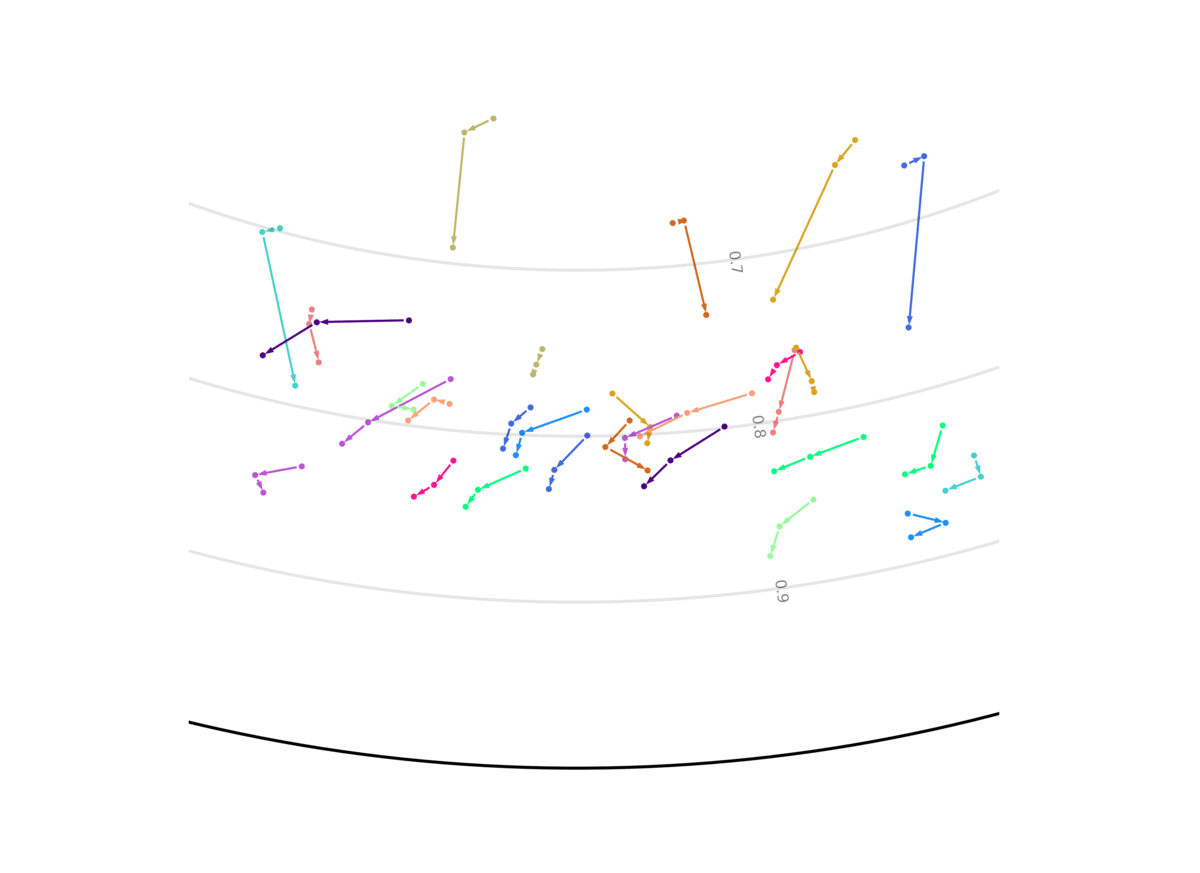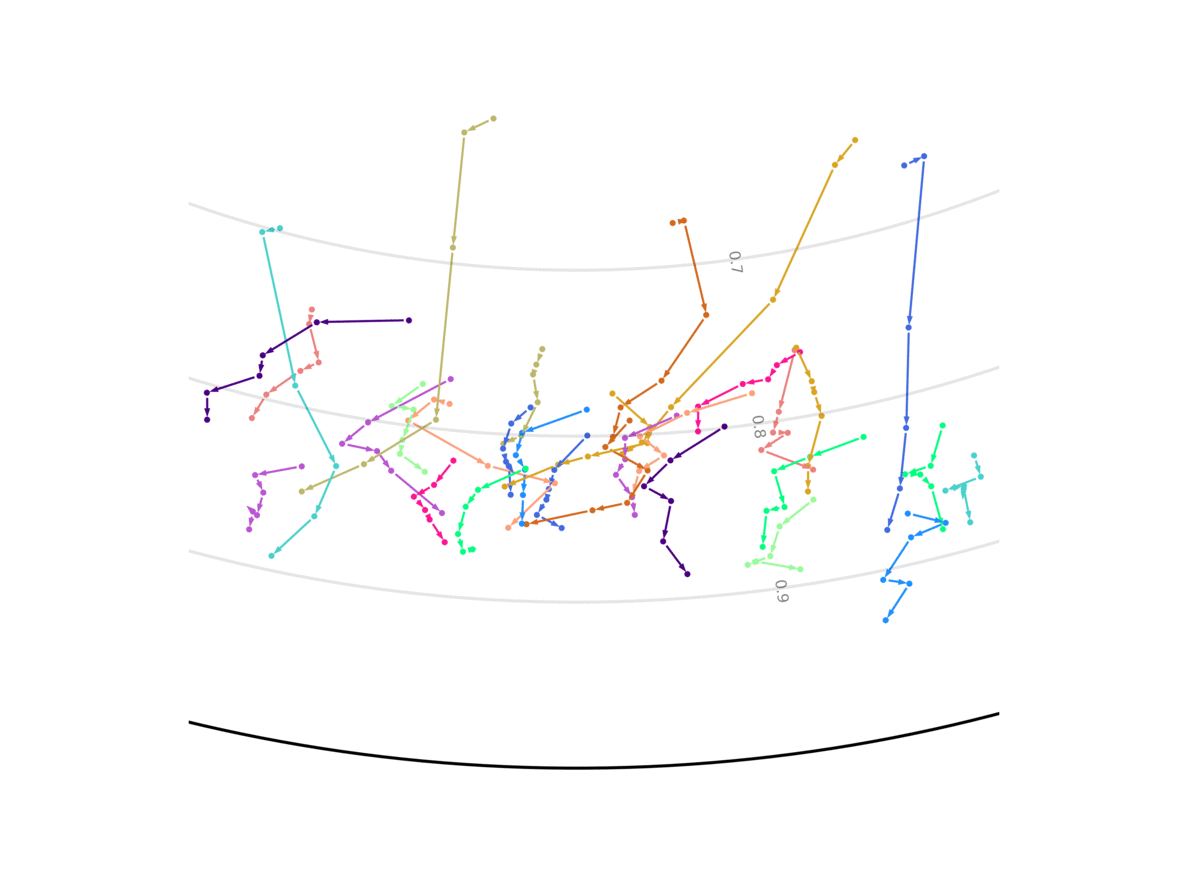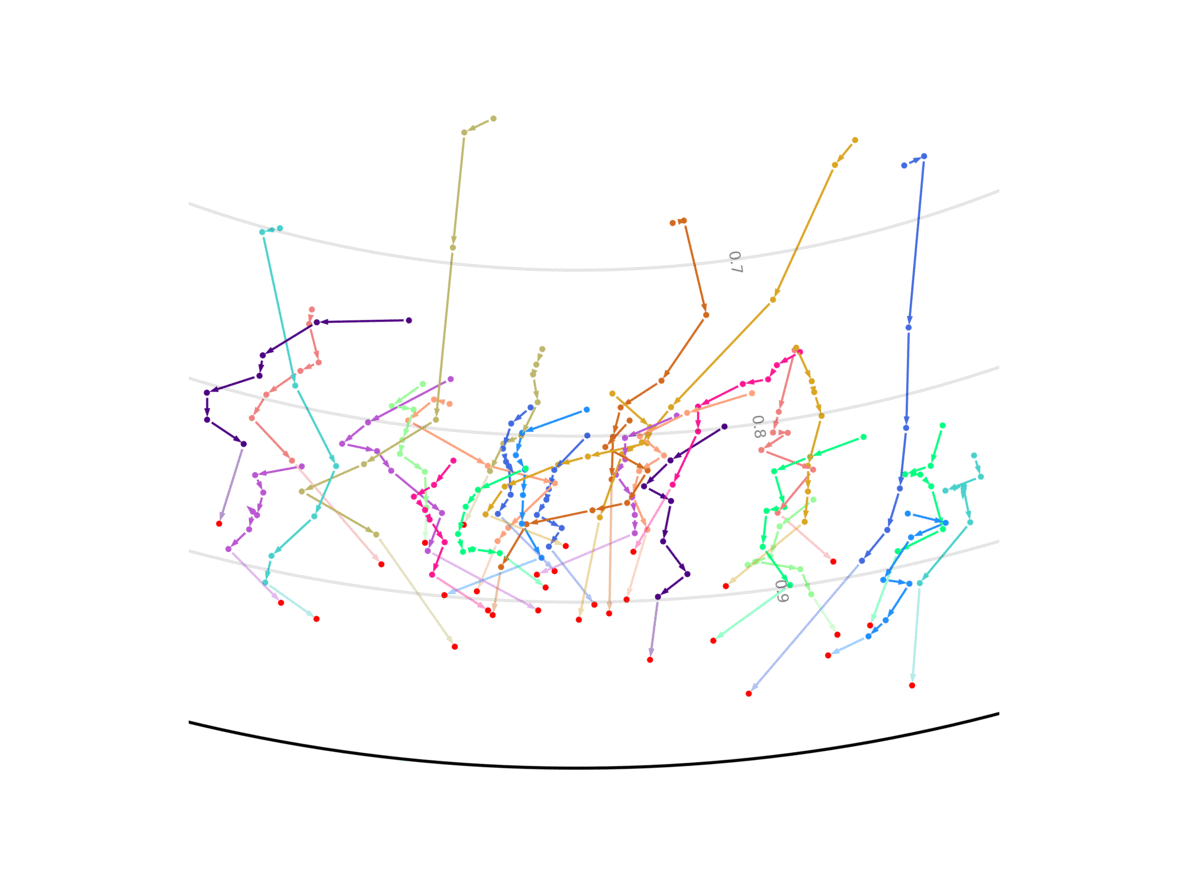
Our model unsupervisedly learns to encode uncertain predictions closer to the center of the Poincaré ball, and confident predictions closer to the edge of the ball. This figure shows the evolution of the representation the more information the system gets, and the closer it is to the future it has to predict. We show two out of the 256 dimensions.
Code and models
Hyperbolic geometry resources
Blogs and web resources- Hyperbolic Geometry and Poinaré Embeddings - Brian Keng
- Poincaré Disk Visualization - Brian Keng
- NonEuclid: Interactive Javascript Software about the Poincaré Disk Model - Joel Castellanos, Joe Dan Austin, Ervan Darnell
- Hyperbolic Geometry in the Poincaré Disk -- using GeoGebra
- Hyperbolic Embeddings with a Hopefully Right Amount of Hyperbole
- Tessellations of the Hyperbolic Plane and M.C. Escher
Acknowledgements
We thank Basile Van Hoorick, Will Price, Mia Chiquier, Dave Epstein, Sarah Gu, and Ishaan Chandratreya for helpful feedback. This research is based on work partially supported by NSFNRI Award #1925157, the DARPA MCS program under Federal Agreement No. N660011924032, the DARPA KAIROS programunder PTE Federal Award No. FA8750-19-2-1004, and an Amazon Research Gift. We thank NVidia for GPU donations. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of the U.S. Government. The webpage template was inspired by this project page.